Combination Formula
The combination formula describes the possible combination of elements out of a group of elements where order does not matter. See the permutations formula for where order does matter.
Formula Terms
| Expression | Description |
|---|---|
| The total number of elements in the group | |
| The number of elements to select | |
| Factorial operator |
The combination formula calculates the possible combinations of elements out of a group of elements where order does not matter. For example, the possible combinations of choosing items from elements is calculated using the expression below.
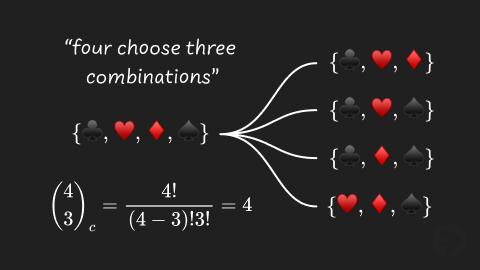
There are possible combinations of choosing items from elements. We can visualize this example using the four suits of a deck of cards represented by the set {♣️,♦️,♥️,♠️}. The possible combinations of “four choose three” are shown below.
- { ♣️, ♦️, ♥️ }
- { ♣️, ♦️, ♠️ }
- { ♣️, ♥️, ♠️ }
- { ♦️, ♥️, ♠️ }
To calculate the possible combinations of choosing two items from the set {♣️,♦️,♥️,♠️}, substitute into the equation for the size of the set and into the equation for the number of items we are choosing.
Evaluate the subtraction, expand the factorial operator, and simplify the fraction.
There are possible combinations of choosing two items from the set {♣️,♦️,♥️,♠️}. This can be seen in the list of possible combinations shown below.
- { ♣️, ♦️ }
- { ♣️, ♥️ }
- { ♣️, ♠️ }
- { ♦️, ♥️ }
- { ♦️, ♠️ }
- { ♥️, ♠️ }
The permutation formula calculates the possible permutations of r elements out of a group of n elements where order does matter.
The number of permutations of n distinct items is given by n factorial. A permutation is a unique ordering or arrangement of the set of items.