Circumference of Circle Formula
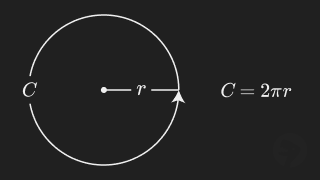
This formula calculates the circumference of a circle in terms of the constant (pi) and the radius of the circle.
Formula Terms
| Expression | Description |
|---|---|
| Circumference of the circle | |
| The circle constant (pi), where | |
| The radius of the circle |
To calculate the circumference of a circle, multiply the circle constant (pi) by two times the radius of the circle. For example, to find the circumference of a circle with a radius of length the formula is:
To find a numeric answer, substitute the value in for the constant and evaluate the multiplication.
The circumference of a circle with a radius of length is equal to units.
The formula for the circumference of a circle in terms of its radius comes from the definition of the constant (pi). The constant is defined as the ratio of any circle’s circumference divided by its diameter. This is illustrated in the figure below.
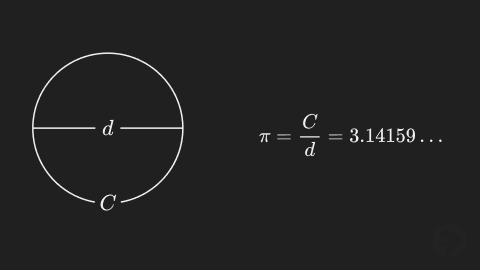
To derive the formula, substitute for the diameter in the definition of and rearrange the equation to solve for the circumference.
The area of a circle is given by the geometric constant π (pi) multiplied by the radius of the circle squared (A = πr²).