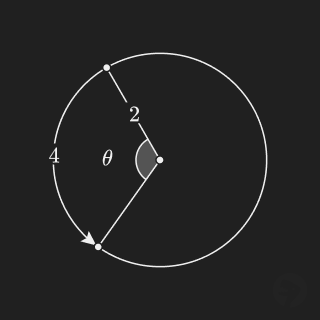
The radian angle system is a unit of measure for angles. To measure an angle in radians, divide the arc length of the angle by the radius used to draw the arc.
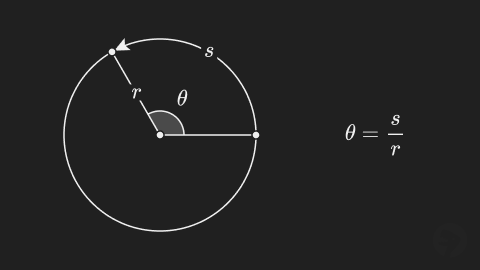
Typically, angles measured in radians are measured in terms of the circle constant (pi) which is equal to a half rotation or .
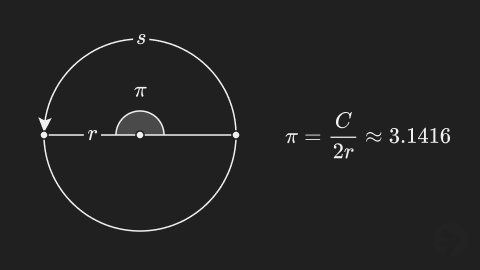
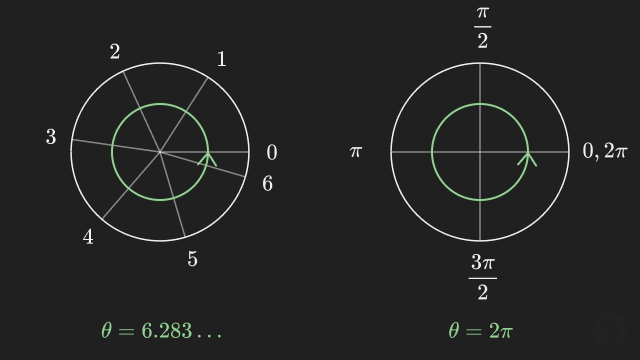
For example, a full rotation is written as radians rather than the decimal value that results from dividing the circumference of a circle by its radius. Both values express the same angle in radians, but using the circle constant is simpler and more clear for special angles.
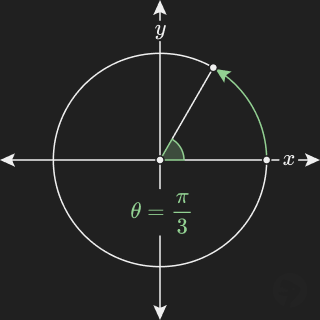
By convention, the positive direction for angles in the -coordinate plane is the counter-clockwise rotation. For example, the angle is drawn starting from the positive -axis and rotating counter-clockwise as illustrated below.
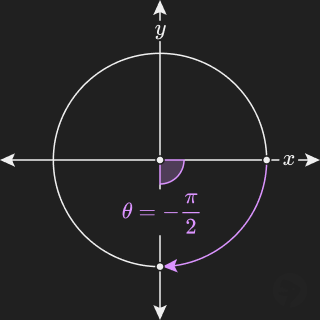
A negative angle like is drawn starting from the positive -axis and rotating clockwise as illustrated below.
The radian system is the unit of choice for measuring angles in math, because it leads to more elegant and concise formulas. For example, the derivative of the sine function is simpler when the angle is expressed in radians[1]. That said, the degree angle system is still widely used throughout math and its good to understand both systems.
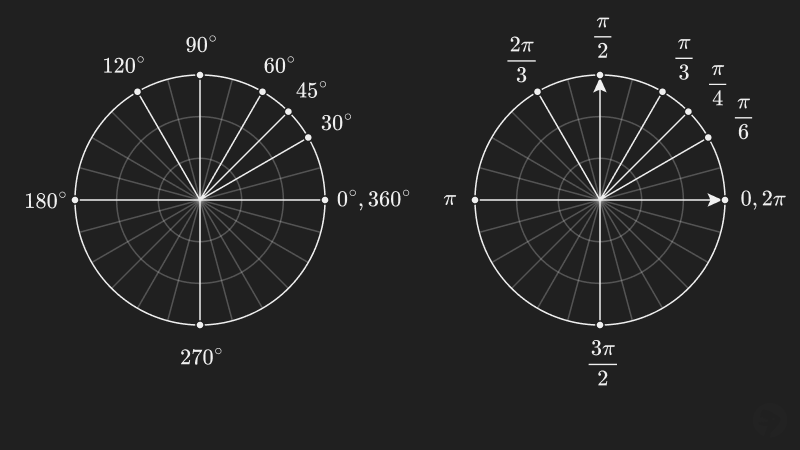
To convert an angle from degrees to radians, multiply the angle by radians over . For example, to convert to radians, multiply by .
Degrees are a unit of measure for angles. A full rotation is equal to 360 degrees. In the XY Cartesian Coordinate System, degrees are measured starting from the rightmost edge of the circle.
The circle constant τ (tau) is a geometric constant approximately equal to 6.283. The numeric value is defined as the length of any circle's circumference divided by the length of its radius.
The Greek letter π (pi) is a geometric constant approximately equal to 3.1416. Its value is equal to the length of any circle's circumference divided by its diameter.
-
Radians Versus Degrees